#数学 ごごごご!物理学者に喧嘩を売るようなタイトルにびびる→物理学者は、数学者の肩に乗った小人なのか フレンケル教授の「数学白熱教室」最終講義 | 読書 - 東洋経済オンライン http://toyokeizai.net/articles/-/95466 … @Toyokeizaiさんから
#数学 続き。内容的には、「数学の理論物理への応用」の話ではなく、ここ30年位のあいだの顕著な傾向である「理論物理の数学への応用」の話をしています。個人的な感覚では場の理論はもはや普通の数学だと思う。論理的に厳密になっている部分だけが数学ではない(当然!)。
#数学 感覚的に理論物理学者達が数学の研究もしてくれるようになったおかげで、数学者人口が相当に増えたような感じ。実際、数学研究をするために読まなければいけない論文の種類と範囲が広がった感じ。これは研究分野的にはとてもハッピーだし、健全なことだと思います。
気分を変えて #数学 から #数楽 に引っ越すことにした。http://bigthink.com/videos/edward-frenkel-let27s-stop-hating-math …Edward Frenkel: Let's Stop Hating Mathtranscript ありのビデオ
#数楽 第2回関係3次と4次方程式の解法と対称性。実際に計算して観察すれば、3次と4次方程式の解の置換の対称性が「可換群の積み重ね」になっていることがわかる。https://twitter.com/genkuroki/status/668189446005649409 …
#数楽 第3回関係楕円曲線y^2+y=x^3-x^2と保型形式η(q)^2η(q^5)^2を使えば「大予想」の特別な場合を数値的に色々確認できる。https://twitter.com/genkuroki/status/671257536218193920 …https://twitter.com/genkuroki/status/673063466853208064 …
#数楽 第3回関係続き個人的には、フェルマー予想よりもラングランズ・プログラムの一段深い段階の帰結になっている佐藤・テイト予想(フレンケルさんは触れなかった)をついでに数値的に確認してみることがおすすめ。http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf …
#数楽 第3回関係続きフレンケルさんも使っていた「いつものあれ」とは別の楕円曲線y^2=x(x^2+x+1)とη(q)^2η(q^5)^2を数値的に調べてみることもおすすめ。デデキントのη函数の定義はη(q)=q^{1/24)(1-q)(1-q^2)(1-q^3)…
#数楽 第4回関係SO(3)の定義とそれが何かに関する説明https://twitter.com/genkuroki/status/672950008312782848 …SO(3)は実3次元空間の原点を中心とする回転のさせ方全体の集合のなす群。3次元の回転は3つの実数パラメーターで記述される。SO(3)は3次元の実リー群。
#数楽 第3回関係追加フェルマー予想とは、3以上の整数nに対して、方程式X^n+Y^n+Z^nの整数解は自明なものしかないという予想。多項式解に関する類似の予想は高校生レベルで証明できる。http://www.math.tohoku.ac.jp/~ytakao/papers/abc.pdf …
#数楽 第3回関係追加フェルマー予想の複素1変数多項式解に関する類似には分岐被覆のトポロジーを使った証明もある。https://twitter.com/genkuroki/status/665395743344185349 …
#数楽 第3回関係追加ラングランズ対応の可換版は類対論。類対論の最も簡単な場合は平方剰余の相互法則。平方剰余の相互法則から素数分の1の循環小数展開に関するある法則が導かれる。その法則の数値的確認法→https://twitter.com/genkuroki/status/670988044418211840 …
#数楽 第4回関係続きO(3)とSO(3)の関係についてアホなことを述べていたので訂正→https://twitter.com/genkuroki/status/672976180706869248 …
#数楽 第4回関係続きSU(2)の定義とSO(3)との関係に関する説明https://twitter.com/genkuroki/status/672973643287158784 …
#数楽 第4回関係続きSU(3)の話→ https://twitter.com/genkuroki/status/672973643287158784 …SU(3)の単純コルート、単純ルート、基本ウェイトおよび各種格子たち→https://twitter.com/genkuroki/status/673387117477675008 …
#数楽 第4回関係続きリー環 sl_3 の旗多様体上の微分作用素による実現と8次元既約表現のウェイト・ダイヤグラム→https://twitter.com/genkuroki/status/673399707595501568 …
#数楽 第4回関係続きSU(3)を例にラングランズ双対群の構成を解説→https://twitter.com/genkuroki/status/673522933898174465 …
@genkuroki #数楽 訂正。「類対論」は正しくは「類体論」です。類体論がらみの現象の特徴は「素数がある等差数列(たち)に含まれるか否かで何かが決まること」です。素数pに関する1/pの小数展開の((p-1)/2+1)桁目が0と9のどちらになるかもそうなっている。
@genkuroki #数楽 https://twitter.com/genkuroki/status/673830400515444736 …訂正。正しくは y^2+y=x^3-x^2 と η(q)^2η(q^{11})^2 です。
@genkuroki # 数楽 https://twitter.com/genkuroki/status/673834349410648064 …訂正。もちろん、正しくは X^n+Y^n=Z^n です。他にも細かいミスはあると思う。
@genkuroki #数楽 あと、SU(3)の8次元既訳表現の別の簡単な構成の仕方についても説明の追加が必要。復習。SU(3)は複素3次正方行列でその転置の複素共役がもとの行列の逆行列になって行列式が1になるもの全体の集合でした。続く
@genkuroki #数楽 続き。行列と行列式について知っていればわかる話にするつもり。集合sl_3(C)を複素3次正方行列でトレース(対角成分の総和)が0になるもの全体の集合と定めます。これは自然に複素ベクトル空間になっています(実際には複素リー環になっている)。
@genkuroki #数楽 続き。群SU(3)の元gは複素ベクトル空間sl_3(C)にA→gAg^{-1}によって自然に作用しています。これで、群SU(3)のsl_3(C)での表現が構成されました。sl_3(C)は8次元既訳表現になっています。続く
@genkuroki #数学 実はこうやって作られるSU(3)の8次元既訳表現のウェイト・ダイヤグラムが、フレンケルさんによる第4回目の話に出て来た「ハドロンの分類図」の数学的正体になっています。あとはウェイト・ダイヤグラムについて説明すればよい。続く
@genkuroki 対角行列A,Bの内積を(A,B)=(ABのトレース)と定めると(H_k,H_k)=2,(H_1,H_2)=-1となる。図を描くときには内積から角度や長さを決めることになる。続く
@genkuroki #数楽 α_{ij}=E_{ii}-E_{jj}と定めると、i≠jのとき、対角行列Hに対してHE_{ij}-E_{ij}H=(H,α_{ij})E_{ij},HH_k-H_k H=(H,0)H_k,が成立することを計算で示せます。続く
@genkuroki #数楽 この事実を、E_{ij}とH_kのウェイトはそれぞれα_{ij},0であるといいます。6個のα_{ij}たちと2つの0を内積を考慮して平面にプロットすると、α_{ij}たちが正六角形の頂点に描かれ、中心に2つの0が描かれます。続く
@genkuroki #数楽 α_{ij}と0の代わりに、E_{ij}とH_kを描いてもいいでしょう。そうやって描かれた図がSU(3)の8次元既訳表現のウェイト・ダイヤグラムであり、フレンケルさんの話に出て来た「ハドロンの分類図」の数学的正体でもあります。
@genkuroki #数楽 i≠jに対するα_{ij}たちをsl_3のルートと呼び、それら全体の集合をルート系と呼びます。この場合にはルート系とコルート系は同じものになる。ルート系は対称性の遺伝子のような役割を果たしています。私はルート系が出て来る数学が大好きです。
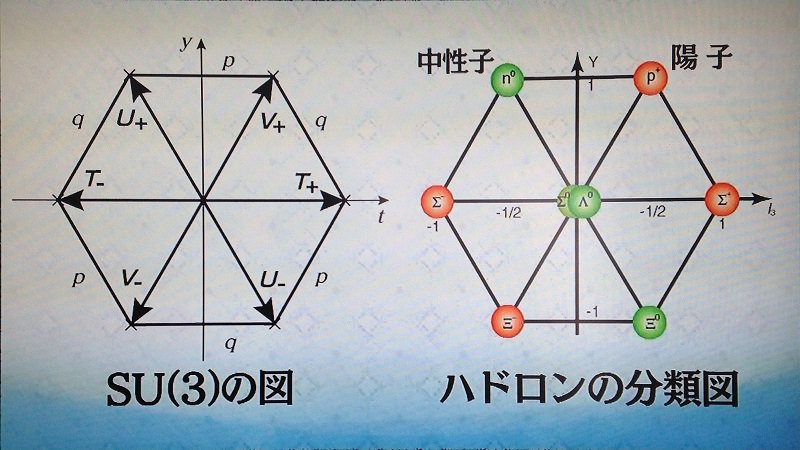
@genkuroki #数楽 pic.twitter.com/jzmNL0DJWK添付図は数学ミステリー白熱教室第4回より。こういう図はトレースが0の3×3行列のある基底からも作れることを以上の連続ツイートで説明しました。大して難しい話ではないです。
@genkuroki #数楽 エドワード・フレンケルさんも若いときに以上で説明した3×3行列たちの地道な計算をやったことがあるはずです。フレンケルさんもたどったはずの地道な計算を自力でたどってみれば、数学ミステリー白熱教室をもっと楽しめると思います。手が届く計算のはずです。

#数楽 pic.twitter.com/jzmNL0DJWK添付図は数学ミステリー白熱教室第4回より。昨晩はこの「ハドロンの分類図」がSU(3)の8次元既約表現のウェイトダイヤグラムになっていることを説明しました。単なる計算としては3×3行列の計算をしまくるだけなので簡単。続く
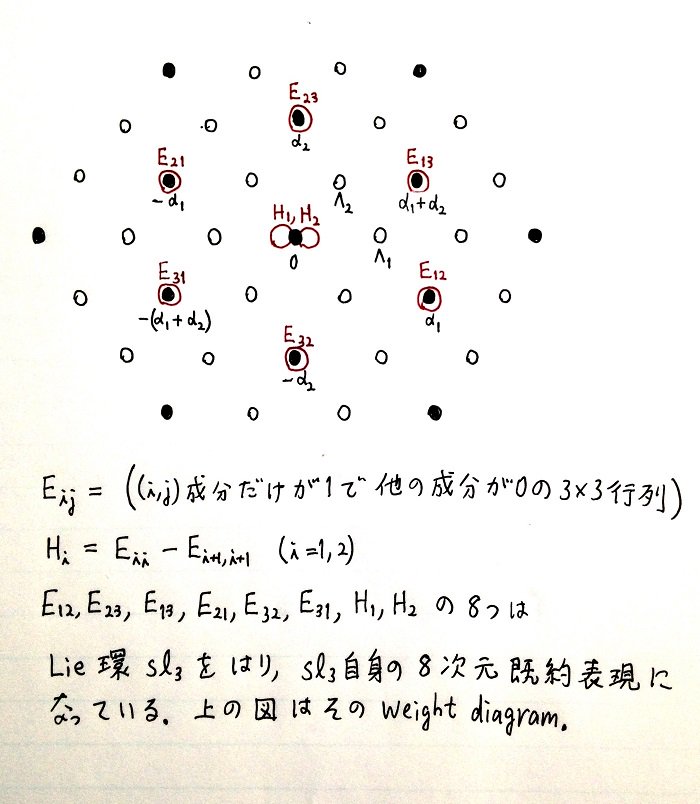
#数楽 続き。問題はその計算と物理の関係です。そのためには量子力学の数学的枠組みの知識が必要になります。まず計算の仕方の復習。添付図は昨晩の計算から得られるウェイトダイヤグラムの図。pic.twitter.com/EWXzPxG8wG

#数楽 pic.twitter.com/EWXzPxG8wGE_{ij}とH_kの定義は添付図を参照。以下3×3行列A,Bに対して、[A,B]=AB-BA、(A,B)=(ABのトレーズ)←内積、α_{ij}=E_{ii}-E_{jj}とおきます。続く
#数楽 i≠jに対するα_{ij}たちの内積を計算すると、各々の長さは√2で、互いの角度は60°または120°になっていることを確認できます。だからそれらは正六角形の頂点に位置していることになります。これが「ハドロンの分類図」で正六角形が出て来る数学的理由です。続く
#数楽 α_{ij}たちはそれでは何なのか?それらはルートと呼ばれています。α_{ij}たちは3×3の対角行列Hについて[H,E_{ij}]=(H,α_{ij})E_{ij}を満たしています。この式はHのE_{ij}への作用の固有値が(H,α_{ij})になると読めます。続く
#数楽 E_{ij},H_kたちはSU(3)の8次元既約表現の基底になっていたのでした。しかもその基底は対角行列HによるA→[H,A]なる一次変換に関する固有ベクトルになっています(固有値はそれぞれ(H,α_{ij}),0)。続く
#数楽 量子力学では固有ベクトルと固有値は純粋状態と観測値に対応しているのでした。α_{ij}たちは複数の対角行列Hの作用の固有値の情報をすべて持っています。だからα_{ij}たちの図(ウェイトダイヤグラム)を描くことは観測値で純粋状態を分類した図を描くことに等しい。
#数楽 数学者の側は対称性に含まれる互いに可換な作用素の組で極大なものを分類し、互いに可換な作用素を同時対角化するという常に重要になりそうなことをまとめて実行しようとします。そういう過程で自然に様々なウェイトダイヤグラムが描かれることになります。
#数楽 物理学者の側は膨大な量の実験・観測を整理することによってハドロンの分類図を得ていた。そして、数学者が得ていた図と物理学者が得ていた図が一致していた!そういう話をフレンケルさんはしていたわけです。数学サイドの計算だけなら3×3の行列の計算ができれば簡単に確認できます。
@genkuroki #数楽 「ハドロンの分類図」と3つのクォークたちが作る3次元既訳表現の関係を説明するためには、表現のテンソル積の分解について説明する必要があるのですが、結構面倒。誰かやってくれないものか。
リンクがうまくいかなかったので再投稿。数学ミステリー白熱教室の再放送の要望。 100Eね! をあつめて再放送を実現しよう! #Eテレ #etv #nhk_rerun #nhk http://www.nhk.or.jp/e-tele/onegai/detail/57015.html … #数楽 #数学
#数楽 #数学 #掛算 数学ミステリー白熱教室!100Eね! をあつめて再放送を実現しよう! #Eテレ #etv #nhk_rerun #nhk http://www.nhk.or.jp/e-tele/onegai/detail/57015.html …
#数学 #数楽 【数学ミステリー白熱教室】登録無しでワンクリックするだけ!100Eね! をあつめて【数学ミステリー白熱教室の】再放送を実現しよう! #Eテレ #etv #nhk_rerun #nhk http://www.nhk.or.jp/e-tele/onegai/detail/57015.html …
#数楽 数学ミステリー白熱教室を見逃した人(投票するべし→ http://www.nhk.or.jp/e-tele/onegai/detail/57015.html … )はE.フレンケルさんの著書Love and Mathの邦訳を読めば内容的にどういう話だったかわかります。 http://www.amazon.co.jp/dp/4163902805 続く
#数楽 http://www.amazon.co.jp/dp/4163902805 この本は原題がLove and Mathなのですが、タイトルから受ける印象とは違って、数学そのものの話が相当に書いてあります。E.フレンケルさんのこの本の印象はひとことで言えば「怖いもの知らず」。続く
#数楽 http://www.amazon.co.jp/dp/4163902805 ある種の数学者集団の中では常識だけど、その外ではほとんど知られていない数学的に基本的な概念が、結構ガチで解説されていたりする。この本を読んだ後に「数学が詳しい友人」に解説してもらえれば理解できることは多いと思う。続く
#数楽 続き。問題は「数学が詳しい友人」をどうやって作るかなのかもしれませんが。E.フレンケルさんの好印象な所は(何度も繰り返して言っていることですが)数学そのものの内容を何とかして伝えようとしていて、最終的に難しい話もしちゃっている所だと思います。続く
#数楽 続き。テレビの数学ミステリー白熱教室でも案の定話が難しくなりすぎて寝ている受講者がテレビにうつっていた。しかし、ツイッターでの感想を見ると、むしろ、わからなさも含めて楽しんでいる人が多い。続く
@genkuroki 話の飛躍があったんですね。多分そのせいで私はあの番組を「分かる人にだけ分かる授業で見る必要が無い」と思いました。分からないことは後で理解しようとするのなら良いですが、下手するとトンデモと区別できない人になりそうな気がします。
@balsamicose 最先端研究の一般向けほ解説で話が飛ばないわけがない。当たり前のこと。たぶん「わからなさ」に耐性がない人はあらゆる分野の最先端研究の動向に触れる機会を大幅に逸すると思う。 #数楽 #数学 #研究 メンションを外して続く
@genkuroki #数楽 実は #数学 の話を聞いた人が難しく感じるのは、話が飛んだ所ではなく、テクニカルは部分を飛ばさずに説明した部分。単なるお話だと思えば難しくないが、「自分でやってみろ」と言われると途端に難しく感じられるようになる。続く
@genkuroki #数楽 ←最近このタグで紹介したように、E.フレンケルさんはテクニカルな面で高校生にも手が届くような数学的な例を結構出していました。話は飛んでなくて、自分にも手が届くかもしれない話をしていることに気付いた人は、わらかなくても心で楽しめたと思う。
@genkuroki #数楽 数学だと、特別な道具は何もいらなくて、考える能力だけがあればよい。 #数学 の世界を本気で見せたいと思ったら、話を聞いている人たち自身の考える能力を発動させる方針を取らざるを得ないんですね。その点について、フレンケルさんはうまくやったと思います。
@genkuroki #数楽 で、現実には、考える能力のうまい発動の仕方を、話を聞いている側はわからないことが多い。そこで齟齬が生じる。しかし、話を聞く側による考える能力の発動を期待していないような話の仕方をすることを、誰が望む?多分そう望む人は最初から話を聞こうとしないと思う。
@genkuroki #数楽 E.フレンケルさんの話を楽しんで聞けた人たちは、自分自身の考える能力の新たな発動を望んでいた人たちだと思う。実際にはうまく発動できなくても、自分にも手が届く所に素晴らしい世界が存在することを確信できた人たちがたくさんいたことを検索で確認できた。



